Originally by Kurt Krempetz for AMA Glider
A combination of launching height and sink rate is what determines how long a glider will stay aloft (glide time, assuming no thermals). If one assumes a particular height, then the sink rate of the glider is what determines the time a glider stays up. Understanding the parameters/issues that increase the sink rate is the ultimate goal. This article is applicable to both indoor catapult gliders and outdoor catapult gliders events, since the fundamental laws of physics stay the same. This article also assumes still air and does not take into account thermals.
Glide Angle
First, one must start with a simplified picture of the forces on a glider as it descends down. We will assume a constant sink rate, with the glider traveling in a straight line, in calm air. The diagram below shows the force on the glider at the CG (center of gravity).
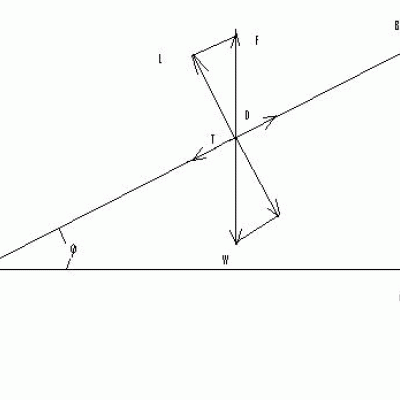
Equation #9 By observing the velocity triangle above, we can see that;
V = Vx/cosj
Equation #10 And
V = Vy/sinj
Equation #11 Substituting into equation #8, we conclude:
Vx = cosj * (2 * W * cosj /(Cd * r * A)) 0.5
Equation #12 And
Vy = sinj * (2 * W * sinj /(Cd * r * A)) 0.5
Now, we have two equations that will predict the horizontal and vertical velocities of the glider. The sink rate is basically Vy, the vertical velocity of the glider.
Minimizing the Sink Rate
In gliders, we want to make the vertical velocity as small as possible. To achieve this, we must take equation #12 and understand how to make Vy as small as possible.
Equation #13 First, we can use equation #3 and rewrite it as:
Sinj/Cosj = Cd/Cl
Equation #14 Substituting equation #13 into equation #12, we get the following:
Vy = Cd * cosj/Cl * (2 * W* cosj /Cl * r * A)) 0.5
Equation #15 If we assume a small angle of descent, cosj (becomes 1 for small angles) and the equation becomes:
Vy = Cd * (2 * W */(Cl * r* A)) 0.5
Equation #16 We simplify and
Vy = 1.41 * Cd * W 0.5/ (Cl 1.5 * r 0.5 * A 0.5)
Equation #17 If we assume a specific design with a fixed weight /area and same air density then:
Vy proportional to Cd/Cl 1.5
To minimize the sink rate, the ratio Cl 1.5/Cd must be as large as possible.
Determining Cl and Cd
One may wonder how to obtain reasonable numbers for Cl and Cd. Airfoils have corresponding data, which are referred to as polars. Polars are basically x-y graphs of Cl vs. angle of attack and Cd vs. angle of attack. Or quite often, polars can be Cl vs. Cd. Polars can either be measured in wind tunnels or theoretically calculated. Since I could not find any wind tunnel testing on model glider airfoils, especially at the Reynolds numbers of interest, I resorted to theoretically calculations. Xfoil is a free 2D software package available on the Internet from Mark Drela. Mark is a professor at MIT and a well-known modeler.
Below are polars for Stan Buddenbohm’s Lit’l Sweep airfoil generated by Xfoil.
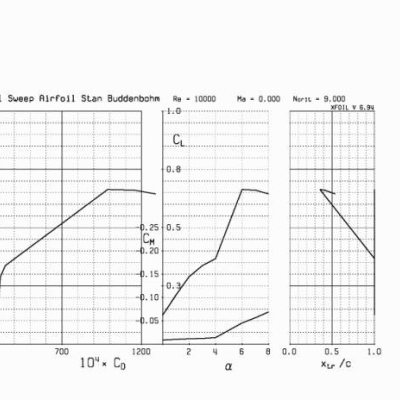
Some equations and spreadsheets were developed to predict sink rate or glide times. The sink rates these equations and spreadsheets appear to give are reasonable, with actual times that are achieved by gliders. It is clear that further work is needed to understand how to predict sink rates. This was a very simple model, in which only the wing (area and airfoil) and weight of the model was included in the calculations. The spreadsheet needs to be developed to incorporate the other factors, which include the elevator, rudder and fuse.
For more articles about model aircraft, please visit AMA Glider’s website.
